소개
LCA란 트리에서 두 노드의 가장 가까운 공통 조상을 찾는 알고리즘이다.
그렇다면 LCA가 필요한 이유는 무엇일까?
바로 설명하자면 트리에서 최단 경로를 LCA로 구하기 때문이다.
트리에서 두 노드 u, v의 최단 경로는 u->LCA + LCA->v 이다. (조금 생각해보면 트리의 성질에 의해 당연하다는 것을 알 수 있다.)
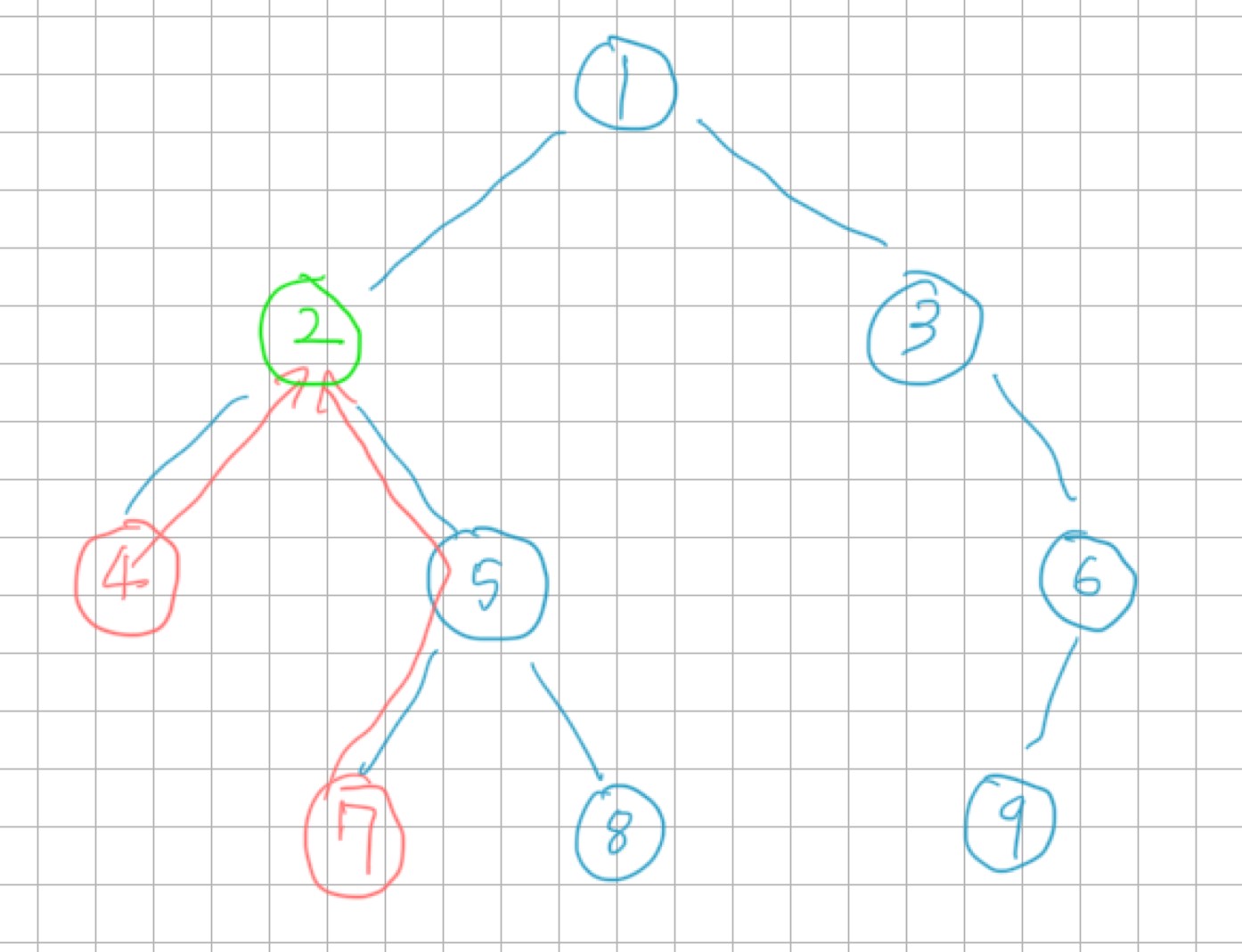예시: 4와 7의 LCA는 2고 최단 경로는 4-2-5-7이다.
그럼 LCA를 어떻게 구할 수 있을까?
접근
첫 번째 방법
naive한 접근으로는 두 노드를 만날 때까지 한 단계씩 옮겨주는 방법을 생각해 볼 수 있다.
- DFS로 트리를 빌드할 때 노드마다 깊이를 기억해 둔다.
- 두 노드가 같아질 때까지 더 낮은 노드를 끌어올린다.
간단하게 코드로 설명하자면 아래와 같을 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
const int MAXN = 50001;
int depth[MAXN]; // 노드의 깊이
int parent[MAXN]; // 노드의 부모
int lca (int u, int v) {
while (u != v) {
if (depth[u] < depth[v]) v = parent[v];
else u = parent[u];
}
return u;
}
이런 방법으로 풀 수 있는 기본 문제가 있으니 시도해보자.
[expand]summary: 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
using namespace std;
typedef long long ll;
typedef vector<vector<int>> adj_list;
const int MAXN = 50001;
int depth[MAXN];
int parent[MAXN];
void dfs (adj_list& G, int now, int par=-1, int d=0) {
parent[now] = par;
depth[now] = d;
for (int child: G[now]) {
if (child != par) dfs(G, child, now, d+1);
}
}
int lca (int u, int v) {
while (u != v) {
if (depth[u] < depth[v]) v = parent[v];
else u = parent[u];
}
return u;
}
int main() {
fastio;
int N; cin>>N;
adj_list G(N+1);
for (int i=0; i<N-1; i++) {
int u, v; cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs(G, 1);
int M; cin>>M;
while (M--) {
int u, v; cin>>u>>v;
cout<<lca(u, v)<<endl;
}
}
[/expand]
두 번째 방법
첫 번째 방법의 문제는 무엇일까?
시간복잡도가 트리의 깊이에 비례하는 것이다.
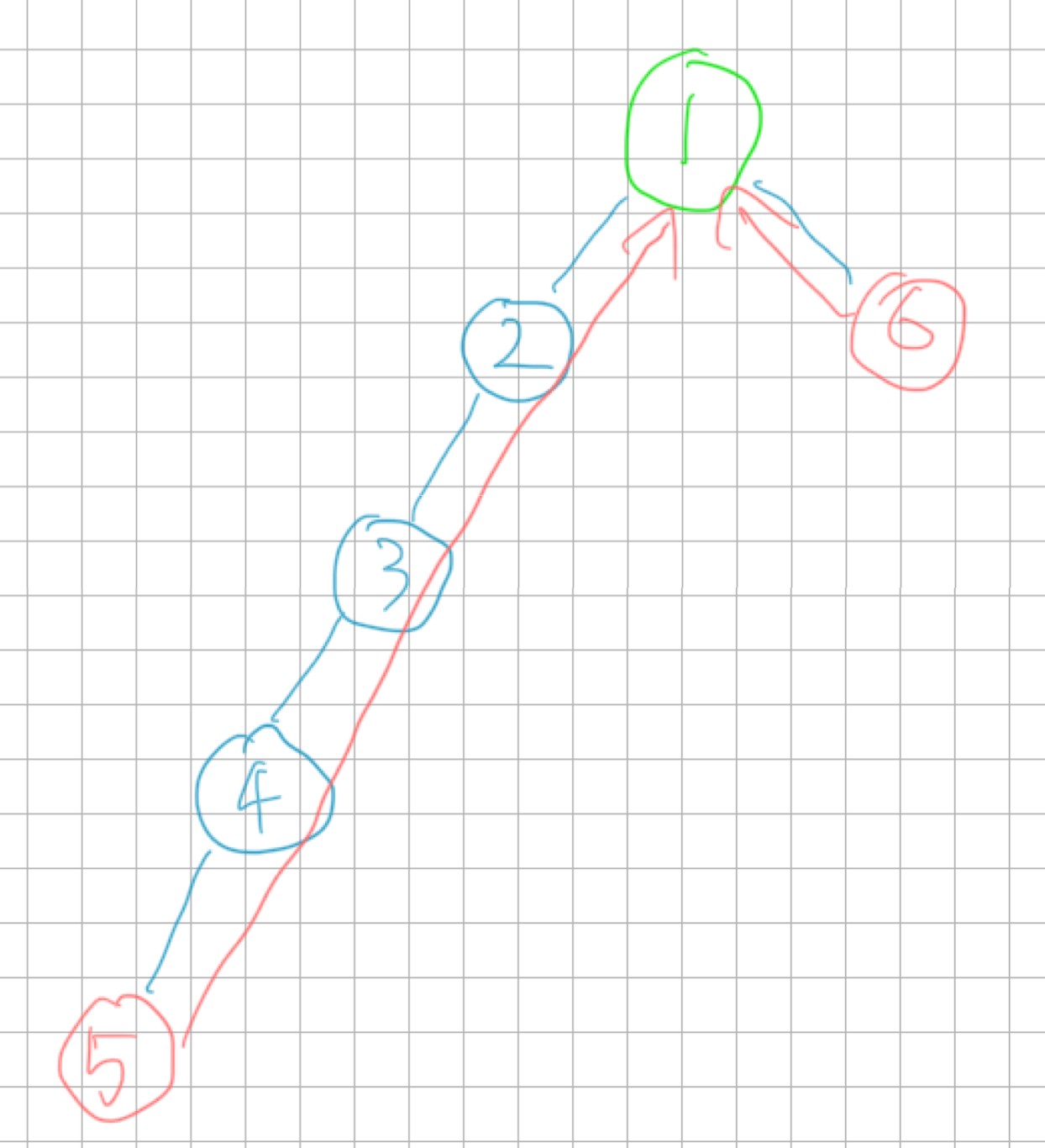
트리가 잘 균형 잡혀있다면 문제가 없겠지만 위 그림과 같은 극단적인 경우 O(N)에 가까워진다. 따라서 다른 방법의 접근이 필요하다.
트리에서 부모를 향해 이동하는 것은 탐색이 아니라 단순히 한 경로만을 타고 올라가는 것이다. 언제 탐색하든 같은 결과를 얻을 수 있다.
따라서 우리는 메모리를 써서 DP처럼 이 문제를 다룰 수 있다.
- cost의 대부분은 높이를 맞춰주는 부분에서 발생한다. (높이가 같아진다면 그때부터 root까지는 최대 log N의 높이를 가지기 때문)
- 높이를 빠르게 맞추기 위해, 1번 위의 조상, 2번 위의 조상, 4번 위의 조상, 8번 위의 조상, …, 2^n번 위의 조상을 기록해 놓는다.
- 탐색 시 더 낮은 노드 u에서 높은 노드 v로 끌어올리기 위해, v의 높이 이하이며 최대한 높은 u의 조상으로 이동을 반복한다.
- 높이가 같아지면 첫 번째 방법과 똑같이, 두 노드가 같아질때까지 둘다 끌어올리면 된다.
위 그림을 기준으로 생각해보면 아래와 같이 진행된다.
- 5의 1번째 조상(4), 2번째 조상(3), 4번째 조상(1) 중 6의 높이 이하인 가장 높은 노드는 2번째 조상(3)이므로 3으로 이동
- 3의 1번째 조상(2), 2번째 조상(1) 중 6의 높이 이하인 가장 높은 노드는 1번째 조상(2)이므로 2로 이동
- 높이가 같으므로, 만날 때까지 두 노드를 끌어올리기
아래는 LCA 2 문제를 해결한 소스다. 참고하며 읽으면 도움이 될 수도 있다.
[expand]summary: 코드 보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
##include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
using namespace std;
typedef long long ll;
typedef vector<vector<int>> adj_list;
class LCA {
vector<int> depths;
vector<vector<int>> ancestors;
public:
LCA (adj_list& tree, int root) {
// 양방향 리스트로부터 LCA 트리 빌드하기
// ancestors[i] = 2^i번째 조상
int N = tree.size();
ancestors = vector<vector<int>>(N);
depths = vector<int>(N);
queue<int> q; q.push(root);
ancestors[root].push_back(root);
while (!q.empty()) {
int now = q.front(); q.pop();
int depth = depths[now];
for (int i=1, d=2; d<=depth; d<<=1, i++) {
ancestors[now].push_back(ancestors[ancestors[now][i-1]][i-1]);
}
for (int child: tree[now]) {
if (ancestors[now][0] == child) continue;
ancestors[child].push_back(now);
depths[child] = depth+1;
q.push(child);
}
}
}
int find(int u, int v) {
if (depths[u] < depths[v]) swap(u, v);
// ancestors를 이용해 끌어올리기
int dv = depths[v];
while (depths[u] > dv) {
int diff = depths[u] - dv;
int jump = 0, jumpd = 1;
while (jumpd<<1 <= diff) jumpd<<=1, jump++;
u = ancestors[u][jump];
}
while (u != v) {
int jump;
for (jump=1; jump<ancestors[u].size() && ancestors[u][jump]!=ancestors[v][jump]; jump++);
u = ancestors[u][jump-1];
v = ancestors[v][jump-1];
}
return u;
}
};
int main() {
fastio;
int N; cin>>N;
adj_list G(N+1);
for (int i=0; i<N-1; i++) {
int u, v; cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
LCA lca(G, 1);
int M; cin>>M;
while (M--) {
int u, v; cin>>u>>v;
cout<<lca.find(u, v)<<endl;
}
}
[/expand]
관련 문제
트리의 두 노드간의 거리를 구하는 쿼리들을 처리해야 한다.
LCA 관련 문제의 가장 기본적인 유형인 것 같다.
[expand]summary: 풀이
ancestors를 만들 때, 같은 방법으로 2^i번째 조상까지의 거리를 기록해놓는다.
탐색시 조상으로 이동할 때마다 거리도 같이 계산해준다.
[/expand]
(u, v)간의 경로의 비용을 처리하는 쿼리와, (u, v)간의 경로 중 k번째 정점을 출력하는 쿼리를 진행해야 한다.
[expand]summary: 힌트
최단경로가 u -> LCA + LCA -> v라는 점을 잘 생각해서,
find의 원리를 잘 생각해보면서 두 가지 쿼리를 각각 짜자.
[/expand]
LCA(u, v)를 구하면 되는데, 쿼리마다 루트가 바뀐다.
[expand]summary: 힌트
그려놓고 여러 케이스를 생각해보며 관찰을 열심히 해보자. 파이팅!
(죄송.. 생각보다 쉽게 찾아짐)
[/expand]