개요
5주차 스터디는 누적합 관련 6문제였다.
A번
문제 요약
N개의 정수 중, 모든 서로 다른 위치의 수의 곱들의 합을 구하는 문제
설명
모든 수들의 합을 미리 구해 놓고, (모든 수의 합 - A[i]) * A[i]를 모든 i에 대해 해주면 된다.
B번
문제 요약
직선 위에 신호등이 1간격으로 쭉 있었는데, 그 중 몇 개가 고장났다.
최소 몇 개의 신호등을 수리해야 연속한 K개의 신호등이 존재하게 할 수 있는지를 구하는 문제
설명
부서진 신호등들과 가상의 양 끝점들을 점으로 잡고 생각한다.
투 포인터로 접근해서 각 점들을 포인터 i와 j로 움직인다고 하자.
i와 j 사이에는 항상 K개 이상의 신호등이 존재하면서 최소로 떨어지도록 움직인다.
그럼 현재 두 포인터가 몇 개의 부서진 신호등을 사이에 두는지를 지속적으로 보면서 최소값을 갱신해주면 그게 답이다.
C번
문제 요약
원형으로 점들이 연결되어 있고, 엣지들마다 거리가 주어진다.
그 중 두 점을 골라 만들 수 있는 거리의 최댓값을 구하면 된다.
설명
꽤 참신한 문제인 것 같았다.
원 위에서의 거리는 min(시계방향 거리, 반시계방향 거리)로 구해지는 것을 누적합으로 이용해서,
시계 방향: 누적합으로 i~j
반시계 방향: 한바퀴 전체 거리 - 누적합으로 i~j
이런 식으로 구하면 된다.
최대값을 구하는 것은 B번 문제와 마찬가지로 투 포인터로 구했다.
D번
문제 요약
N개의 수가 주어졌을 때 정수 하나를 빼서, 나머지 수의 최대공약수가 K의 약수가 아닌 수가 되게 만드는 방법을 구하는 문제
설명
아이디어를 떠올리기가 좀 어려웠다.
왼쪽부터의 gcd, 오른쪽부터의 gcd를 구해 놓고
각 i들에 대해 i를 뺀 값을 gcd(left_gcd[1, i-1], right_gcd[i+1, N])로 구하면 된다.
E번
문제 요약
정수 수열을 4개의 구간으로 나눠서, 각 구간의 합이 같게 만드는 방법의 수를 구하기
설명
SCPC 예선에서 풀었던 문제의 쉬운 버전이었다.
그런데 SCPC 예선때 짠 코드가 더럽고 이상해서, (억지로 푼 느낌이어서) 다른 사람 풀이를 봤더니 훨씬 깔끔한 풀이가 있었다.
일단 처음에 푼 방법은, (전체 누적합 / 4)로 나누어떨어지는 위치들과 몫을 구해 놓는다. (안 나눠 떨어진다면 0)
그럼 [1, 1, -1, 1, 1, 1, 1, 1]는 누적합이 [1, 2, 1, 2, 3, 4, 5, 6] 2로 나눠서, [0, 1, 0, 1, 0, 2, 0, 3]처럼 되고,
1중 하나와 2중 하나, 3(항상 마지막이어야 함)을 순서대로 구하는 방법을 구하는 확통으로 접근했다.
근데 문제는, [1, -1, 1, -1, 1, -1, 1, -1]같이 0으로 나눠야 하는 경우는 순서가 없어져서 따로 처리를 해 줘야 했다는 건데,
SCPC때는 급해서 아예 다른 방법으로, 0을 만드는 모든 위치를 이항 계수로 nCr을 구하도록 처리했다.
새롭게 알게 된 풀이는 저렇게 나눠 놓는 게 아니라, i까지의 누적합이 (전체 누적합 / 4) * j 와 같은지를 스위핑과 DP로 세 주는 방법이다.
정말 깔끔하게 풀려서 놀랐다.
DP는 0, 1, 2, 3 이렇게 4칸만 만들어 두고, 각 i에 대해서 몫이 j라면 dp[j]에 dp[j-1]을 더해주면 된다. (LIS처럼)
그 부분의 코드는 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
vector<ll> ans(4);
ans[0] = 1;
for (int i=1; i<N; i++) {
for (int j=3; j>=1; j--) {
if (presum[i] == bucket_val * j) {
ans[j] += ans[j-1];
}
}
}
cout<<ans[3]<<endl;
F번
문제 요약
직선 위에 점들이 있다.
트럭으로 옮기면 (트럭비용 * 개수 * 거리) 만큼의 비용이 발생하고,
헬리콥터로 옮기면 (헬리콥터 비용) 만 발생한다. (개수와 거리에 상관이 없다.)
화물의 목적지의 목록이 주어졌을 때, 모든 화물을 옮기는 최소 비용을 구하는 문제
설명
그리디나 DP로 풀어야 하는 것 같은데 뭔가 아이디어도 생각이 안 나고 풀 의욕도 별로 안 생겼다. 그래서 못 풀었다.
다음에 시간 날 때 업솔빙 해 봐야겠다.
6주차 문제를 풀다가,
중간값이라는 아이디어를 생각하면서 접근했는데도 꽤 어려웠다. (내가 DP에 약한 것 같다.)
이 문제에서는 물품의 목표 지점들 외의 점은 필요가 없다.
(거리가 단순 절댓값이므로, 헬리콥터는 목표 지점 중에서만 골라 보내도 항상 최적값이 나오는 것이 보장된다. 여러 절대값의 합 그래프 개형을 생각해 보자.)
먼저 트럭의 비용을 T, 헬리콥터의 비용을 H, d[i]를 i번 목표 지점이라고 하자
DP[i] = i번 택배까지 모두 보낼 때 최소 비용으로 잡고, DP[i] = DP[i-1] + d[i] * T로 트럭 비용은 계산할 수 있다.
그 다음은 헬리콥터의 비용인데, 헬리콥터는 각각 특정 구간을 맡는다고 생각하면 된다.
(i < j < k 일 때, i와 k만 같은 헬리콥터로 보내는 경우는 없다고 생각해도 된다는 말이다.)
그럼 이제 구간의 비용도 DP로 계산해 주면 되는데, 각 점마다 이전의 모든 점을 보면서, 두 점 사이의 구간을 확인해 주면 된다. (N^2)
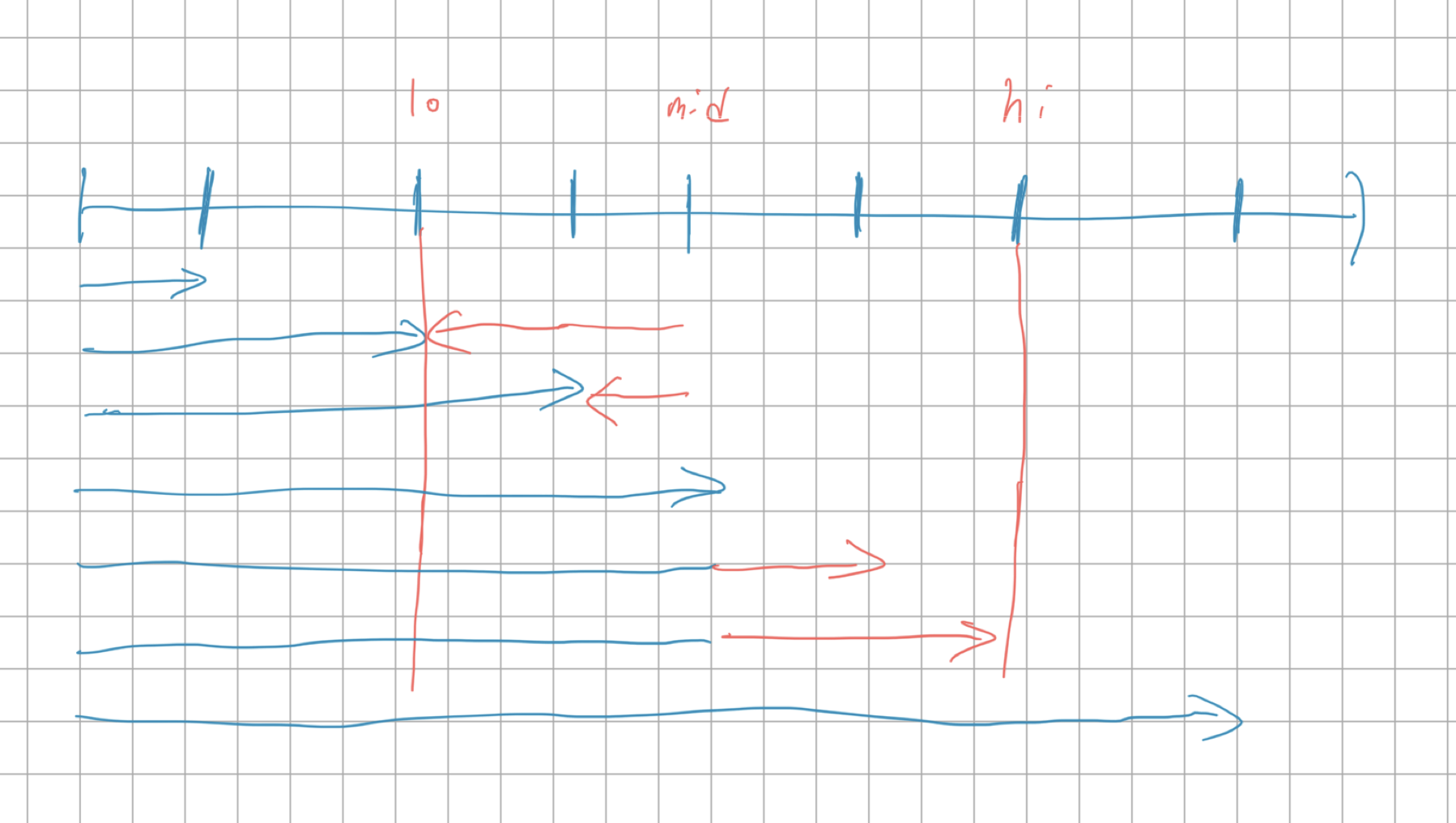그림을 보자. 위에서 말한 두 점(lo, hi)으로 표현되는 구간 하나를 나타낸 것이다.
이제 각 구간의 비용을 계산해야 하는데, [lo, hi]의 모든 점에 대헤 dist(mid, point)의 합을 O(1)에 구할 것이다. (위 그림의 빨간 부분)
위 그림을 보면서 생각해 볼 수 있는 것은 첫 번째로, [lo, mid]에서 끝나는 선분들은 모두 [0, lo]까지의 길이를 공유하고, [mid, hi]에서 끝나는 선분들은 [0, mid]를 공유한다는 것이다.
두 번째는 [lo, mid]에서 끝나는 선분들과 [mid, hi]에서 끝나는 선분들만 보면 된다는 것이다.
그래서, 각 점들을 통해 누적합을 만들어서, 특정 구간에서 끝나는 선분들의 길이의 합을 빠르게 구할 수 있게 한다.
[lo, mid]에서 끝나는 선분의 빨간 부분은 각각 보면 [0, mid] - 파란 선분이다. 따라서 모든 선분이 공유하는 부분 [0, mid]는 d[mid] * [lo, mid]에서 끝나는 선분의 수로 계산해 줄 수 있고, 서로 다른 부분(파란색)은 누적합으로 [lo, mid] 사이에서 끝나는 모든 선분의 길이의 합을 구해 빼주면 된다.
(d[mid] * (mid - lo + 1) - (presum[mid] - presum[lo-1])) * T
[mid, hi]은 좀 더 쉽다. [mid, hi]에서 끝나는 모든 선분들의 길이를 누적합으로 구해서 [0, mid]까지의 공유하는 길이를 모두 빼 주면 된다.
((presum[hi] - presum[mid]) - d[mid] * (hi - mid)) * T;
그럼 헬리콥터의 비용은 위 두 값 + H로 구할 수 있다. DP[lo-1]에 더해주면 된다.
전체 코드는 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define endl '\n'
#define all(x) x.begin(), x.end()
#define sz(x) x.size()
using namespace std;
typedef long long ll;
int main() {
fastio;
int N; cin>>N;
vector<int> d(N+1);
vector<int> presum(N+1);
vector<int> dp(N+1);
for (int i=1; i<=N; i++) cin>>d[i];
int T, H; cin>>T>>H;
sort(all(d));
for (int i=1; i<=N; i++) presum[i] = presum[i-1] + d[i];
for (int hi=1; hi<=N; hi++) {
dp[hi] = dp[hi-1] + d[hi] * T;
for (int lo=hi; lo>=1; lo--) {
int mid = (lo+hi)/2;
int low_dists = (d[mid] * (mid - lo + 1) - (presum[mid] - presum[lo-1])) * T;
int high_dists = ((presum[hi] - presum[mid]) - d[mid] * (hi - mid)) * T;
dp[hi] = min(dp[hi], dp[lo-1] + low_dists + high_dists + H);
}
}
cout<<dp[N]<<endl;
}